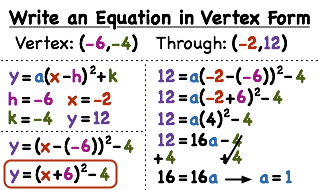
A quadratic equation is a polynomial equation of degree 2, which means the highest power of the variable is 2. It takes the general form:

• ax² + bx + c = 0

Where ‘x’ stands for the variable and ‘a,’ ‘b,’ and ‘c’ are coefficients. Numerous mathematical and practical situations, including projectile motion, geometry, finance, and optimisation issues, include the use of quadratic equations.

What is the vertex form and its coordinates?

A quadratic equation can be expressed in a particular way that emphasizes the vertex’s coordinates, known as the vertex form. The general form of the vertex form equation is as follows:

• y = a(x – h)² + k

Where (h, k) stands for the vertex’s coordinates and “a” is the coefficient before the x2 term.

The x-coordinate and y-coordinate of the vertex point on the parabolic curve are represented by the vertex coordinates, (h, k). Depending on the coefficient “a” and the curve’s shape, the vertex is either the highest or lowest point of the parabola.

In the vertex form equation, the value of “h” is the vertex’s x-coordinate, signifying the parabola’s horizontal shift, and “k” is the vertex y-coordinate, signifying the parabola’s vertical shift. The parabolic curve’s breadth and direction are influenced by the “a” coefficient.

Methods to solve quadratic equation

There are two ways to solve quadratic equation

1. Using Quadratic formula calculator
2. Manually

Solving quadratic equation with quadratic formula calculator

A digital tool known as a quadratic formula calculator automates the process of calculating quadratic equations. The calculator performs the quadratic formula and generates accurate solutions after receiving the equation’s coefficients.

Step by step method

1. Put the quadratic equation’s coefficients “a,” “b,” and “c” into the calculator. These coefficients, in turn, stand in for the numbers in front of the x², x, and constant expressions.
2. Determine the vertex’s x-coordinate by applying the formula h = -b / (2a). Calculate by entering the values of “a” and “b” into the calculator.
3. Determine the vertex y-coordinate, once you know the vertex’s x-coordinate, you may return the original quadratic equation to its original form and evaluate it to determine the vertex associated y-coordinate. You will receive the vertex form value of “k” after doing this.
4. Write the equation in vertex form: You may write the quadratic equation in vertex form as follows using the vertex’s x- and y-coordinates:

  y = a(x – h)² + k.

The vertex’s x- and y-coordinates are represented by the letters “h” and “k,” respectively. “a” stands for the coefficient in front of the x2 term.

You may rapidly determine a quadratic equation’s vertex form by using a quadratic formula calculator. Calculations are automated, lowering the possibility of mistakes and expediting the procedure.

Solving quadratic equation manually

The following steps are often included in the manual method:

1. Simplifying the Formula: Put the quadratic equation in standard form with zeros for all terms on one side.
2. Factoring: Split the quadratic equation into two binomial expressions, if at all possible. When the equation is simple to factor, such as (x + 2)(x – 3) = 0, this method works.
3. Completing the Square: In this method, the equation is changed to produce a perfect square trinomial, and the variable is then solved for. When the quadratic equation is not factorable, it is extremely helpful.
4. Quadratic formula: The quadratic formula is used if factoring and completing the square approaches are not feasible or practicable.

Completing the square method

Here we will elaborate one of these methods i.e. by completing the square

• Start with the quadratic equation ax² + bx + c = 0 in standard form.
• If ‘a’ is not equal to 1, divide the equation by a. The equation’s constant term, “c,” should be moved to the other side.
• To both sides of the equation, add [(b/2a)²].
• Rewrite the equation to (x + b/2a)² = (b² – 4ac)/4a² to make it simpler.
• Simplify by taking the square root of both sides.
• Subtract b/2a from both sides.
• The resulting vertex form equation is x= (-b ± √(b² – 4ac))/2a.

Comparing both methods

You may easily find the vertex form of a quadratic equation by using a quadratic formula calculator. It automates the computations, lowering the possibility of mistakes and speeding up the procedure. Simply enter the coefficients and follow the procedures indicated above to get the quadratic equation in vertex form. On the other hand, manual solution techniques give a thorough understanding of the algebraic procedures involved and can be helpful for instructional purposes or when utilizing a calculator to perform precise calculations is difficult.

While both approaches are acceptable, a quadratic formula calculator offers the ease, speed, and precision that make it the better option when working with challenging equations or when time is of the essence.